Par Jean SANS – cet article est une version revisitée et complétée, notamment dans ses conclusions, de la Partie 2 de l’étude, éditée le 22 janvier 2016 sur www.uncl.com.
Dès que l’on parle de foils sur un voilier, on se met à rêver d’une coque en lévitation au dessus des flots.
Si la phase vol, avec bien sur la phase préalable de décollage, est assez facile sur un multicoque, on comprend rapidement que c’est pratiquement impossible sur un monocoque lesté, surtout s’il est équipé d’une quille.
Je pense que le Moth Foiler est le seul monocoque qui vole réellement et qui peut régater, c’est à dire évoluer librement sur un parcours entre deux ou trois bouées. Pour voler, il faut quitter le régime archimédien, donc soulever et extraire la carène de l’eau. Cela signifie qu’il faut créer une force verticale supérieure au poids du bateau et de son équipage en utilisant la portance générée par les foils.
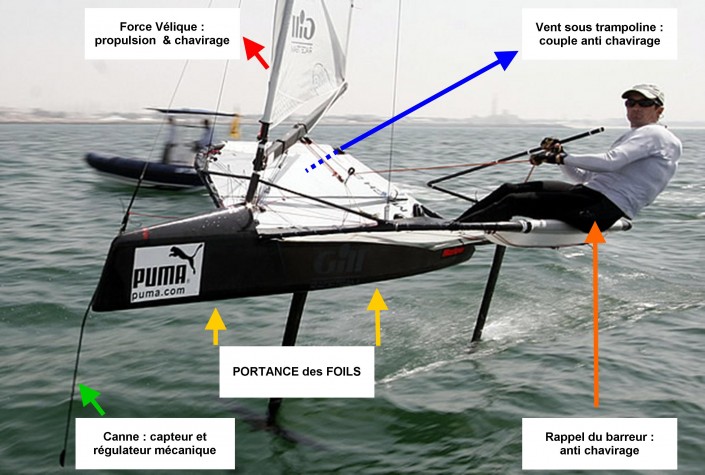
Je rappelle les caractéristiques de base d’un Moth Foiler :
- Longueur de Coque 3.55m,
- Surface de Voile : 8m2,
- Poids gréé : 25kg,
- Déplacement en navigation : 130 kg avec un barreur de 90 kg et des extra, comme 5 litres d’eau dans le bateau par exemple.
Cela signifie que la force verticale est d’environ 60 daN par foil en « T ». Le deux foils en « T » sont régulés mécaniquement (orientation d’un volet sur le bord de fuite), sans aucune énergie électrique. C’est une « vulgaire » canne articulée et immergée à l’étrave qui traine dans l’eau et assure cette fonction de régulation.
Le barreur est un funambule dont le comportement en navigation est plus proche de celui d’un surfeur que de celui d’un navigateur sur un bateau comme on l’entend communément. En comparaison, les utilisateurs de 49ersfont figure de « retraités de la marine ».

Conclusion : le Moth Foiler vole, c’est une réalité, mais la transposition de ce « vol intégral » sur un monocoque lesté, même classé dans la catégorie « super light boats », a toutes les chances de demeurer une utopie.
Pourtant, le Quant 23 qui n’est pas exactement un monocoque, bien qu’il y ressemble, vole aussi (un monocoque doit posséder une carène dont le creux ne diminue pas lorsque l’on se rapproche du plan de symétrie de la carène). En fait, le QUANT 23 possède une architecture de catamaran, comme le montre la vue de droite ci-dessous :


L’architecture navale est quand même une science extraordinaire, car avec des matériaux plus performants que ceux de l’époque, les architectes auraient pu imaginer des foils et faire voler les Scows.
Alors pourquoi des foils sur un quillard et quel(s) effet(s) sur le bateau ?
Contrairement au Moth dont les deux foils se situent dans le plan de symétrie du bateau et assurent une poussée sensiblement verticale, les foils sont implantés latéralement sur un monocoque lesté.
Que se passe-t-il lorsque le foil est actif ?
Dans un premier temps, regardons l’équilibre sous voiles d’un voilier SANS foil :
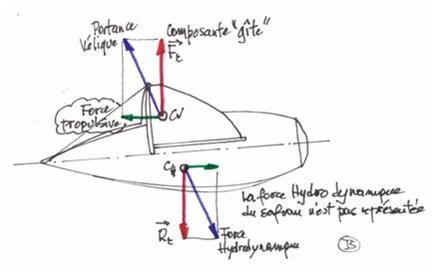
Au regard des forces en présence :
- En transversal, seules les forces Fc et Rt sont prises en compte.
- Ces forces génèrent la gite du bateau.
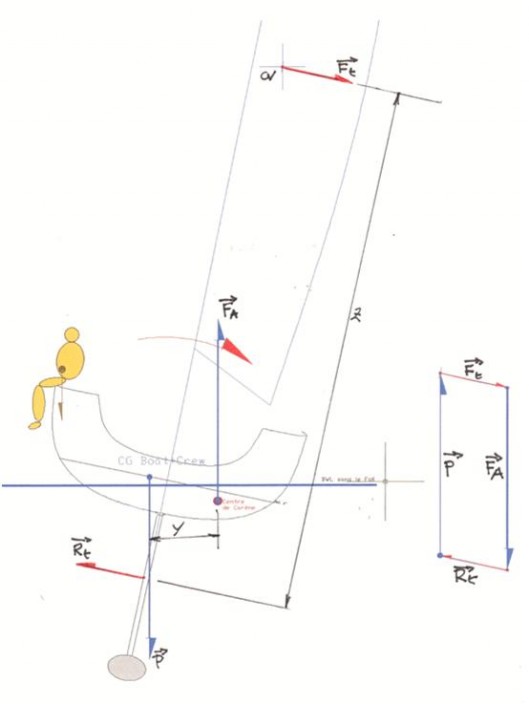
Lorsque l’on regarde l’équilibre du bateau en transversal, les forces appliquées sur un bateau dépourvu de foil sont les suivantes :
- Une composante de la portance « anti-dérive Rt » générée par le voile de quille et aussi le safran.
- Une composante de la « force vélique Ft » qui fait giter le bateau :
- Lorsque le bateau est en équilibre à un angle de gîte, la composante anti-dérive Rt et la composante de la force vélique Ft sont égales et parallèles.
- Dans ce cas les couples Ft * z et P *y sont égaux.
- La force verticale P (dirigée vers le bas) correspond à la masse du bateau, du mât, de l’équipage, de la quille inclinable, des ballasts liquides etc. Cette force correspond au déplacement en navigation du bateau et s’applique au centre de gravité général qui est légèrement excentré par rapport au plan de symétrie du bateau.
- La force verticale Fa (dirigée vers le haut) est produite par la poussée d’Archimède. Cette force s’applique au centre de carène (centre de gravité du volume immergé). Lorsque la densité de l’eau est 1, ce volume est égal au déplacement du bateau en navigation.Le parallélogramme dessiné à droite montre le polygone vectoriel des forces en présence. Comme le bateau est en équilibre, le polygone vectoriel est obligatoirement fermé.
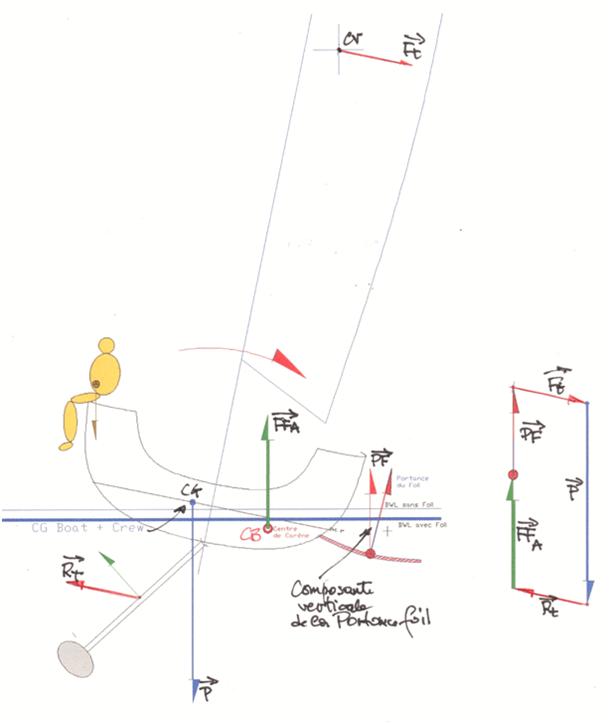
Que devient cet équilibre lorsqu’un foil est déployé ?
Constat : une nouvelle force PF (portance du foil) apparaît. Cette nouvelle force possède une composante verticale. Dans l’exemple ci-contre, j’ai volontairement dessiné la portance verticale.
Nous passons en transversal de 4 à 5 forces, mais comme le bateau est en équilibre statique, le polygone vectoriel doit être fermé.
Cette nouvelle force PF est verticale (enfin sa composante), on doit donc l’intercaler verticalement entre l’extrémité de FFa et le début de Ft.
Comme Ft et Rt sont obligatoirement parallèles, on obtient PF + FFa = P, ce qui signifie que la poussée d’Archimède diminue.
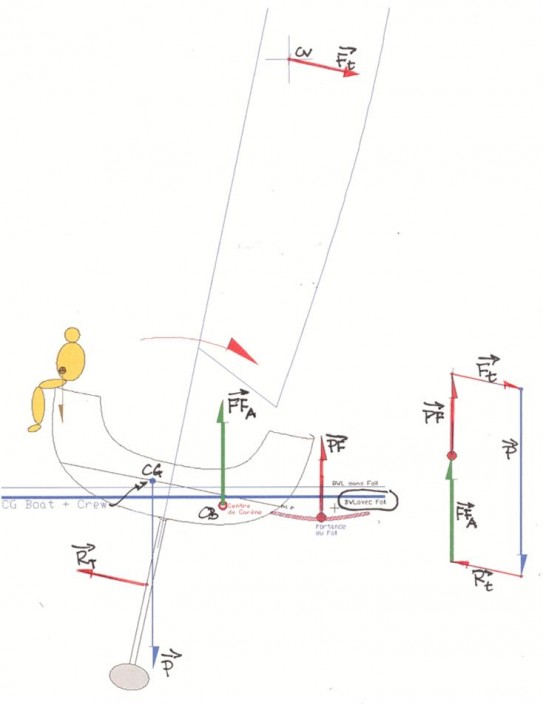
Conclusion : le bateau flotte « plus haut », son déplacement archimédien diminue.
La limite de l’exercice se situe au moment où le foil sort de l’eau, alors le bateau retombe !
Mais une force PF qui « allégerait » le bateau de 10 à 15% devrait normalement améliorer les performances et cela malgré le trainée induite du foil. C’est ce qui fait cogiter les Architectes.
Sur un bateau équipé d’une Canting Keel, l’effet est identique (voir ci-dessous).
Transposition du Moth au monocoque lesté
Le MOTH parvient à « voler » malgré sa largeur assez réduite. C’est un bateau extrêmement léger équipé de plates-formes latérales sur lesquelles le barreur est installé. Le rapport de masse entre barreur et bateau est pratiquement de 3.5 à 1. Le barreur peut donc facilement faire gîter le bateau au vent. Du fait de la contre gîte, la force vélique pointe vers le haut, ce qui diminue la pression sur le foil porteur.
Il faut bien comprendre que maintenir le bateau contre gîté sera la condition sine qua non pour obtenir d’abord le décollage, puis et surtout le vol, c’est à dire la coque entièrement extraite de l’eau.
Alors pourquoi essayer de mettre un ou des foils sur un voilier monocoque lesté ?
Oublions tout d’abord l’idée de copier le MOTH et installer un foil en « T » en bout de quille. En effet, faire contre-gîter un voilier lesté est déjà un rêve, ensuite lui ajouter des plans porteurs symétriques dont l’envergure serait supérieure à la largeur du bateau relève du cauchemar. On peut néanmoins améliorer la performance d’un voilier « lourd « , non pas en le sortant complètement de l’eau, mais en diminuant son volume immergé comme nous venons de le voir graphiquement.
Le décalage du foil sous le vent, et donc de la portance, paraît dans un premier temps être le bénéfice immédiat apporté par le foil. Il est incontestable que le couple de redressement augmente sous l’effet du foil et plus on va vite plus il augmente. On se dit immédiatement que le foil apporte un gain de puissance phénoménal.
Deux calculs rapides à 13 nœuds et à 17 nœuds sur un 53’ (déplacement 9000 Kg) équipé d’un foil type « DSS » de 1.75 m2 avec bras de levier entre le centre de carène et le centre d’application de la portance du foil de 2.5m :
- A 13 nœuds (6.68 m/s)
- la portance est de 1400 daN (approximativement 1.4T)
- le couple de redressement créé de 3500 m * daN
- A 17 nœuds (8.74 m/s)
- la portance est de 2400 daN (approximativement 2.4T)
- le couple de portance créé de 6000 m * daN
Pour information le couple de redressement de ce bateau à 15 ou 20° de gîte avec l’équipage au rappel est de l’ordre de 7500 m*daN.
La vitesse augmente de 31% et le couple de redressement de 71%. Certes c’est une démonstration relativement théorique, mais l’ordre de grandeur de l’effet physique est réaliste. On voit donc, en première approche, que la puissance disponible, c’est à dire la capacité du bateau à porter de la surface de voilure augmente significativement car le foil excentré augmente le couple de redressement. La réaction première est de dire : augmentons la surface de voilure.
C’est là que le bas blesse, car si effectivement il y a création d’un couple de redressement additionnel par le foil, il y a surtout, du fait de la composition des forces dans l’équilibre transversal du bateau (voir le polygone vectoriel), une diminution non négligeable de la poussée archimédienne, donc un soulèvement du bateau… Son déplacement archimédien diminue bien que son déplacement réel ne change pas, la masse du bateau en mouvement ne changeant pas.
Les deux phénomènes sont très imbriqués. Il est acquis que le foil améliore le couple de redressement. Il est démontré que la poussée d’Archimède diminue puisque la somme de cette poussée et de la portance du foil doit être toujours égale au poids du bateau.
Dans ces conditions, la vitesse du bateau augmente (moins de surface mouillée, meilleure aptitude au planning).
Si la vitesse du bateau augmente, la portance vélique augmente (avec, ne l’oublions pas, le carré de cette vitesse), la composante transversale (Ft) de la portance augmente donc de fait, et corolairement le couple de chavirage. Ce couple de chavirage est équilibré par le supplément de couple de redressement généré par le foil puisque la vitesse aidant, la portance du foil a aussi augmenté.
On comprend ainsi que les deux couples s’équilibrent (je pousse…tu t’opposes) et que le phénomène prépondérant qui va permettre d’augmenter significativement la vitesse est la sustentation du bateau et son extraction de l’eau. La quintessence de cet effet étant atteinte lorsque la coque est entièrement hors de l’eau comme sur le MOTH.
Cette transition entre le régime archimédien et le régime « vol intégral », dans lequel toute la carène est subitement hors de l’eau, est très violente. Elle se traduit quasi instantanément par une vitesse multipliée par trois ou quatre, sans aucune progressivité. Certes la perception doit être plus soft sur un monocoque lesté, mais l’effet doit être presque identique à celui que l’on perçoit sur un sportboat quand on enroule la bouée de près et que le spi asymétrique se gonfle par 30 nœuds.
Quels sont les ordres de grandeur possibles pour la portance d’un foil ?
La portance d’une forme aéro ou hydrodynamique est calculée par la formule suivante :
P = ½ * ρ * Cz * S * V2 (Force en Newton).
- V = vitesse de la forme (ici le foil) dans le milieu (eau). Elle s’applique en m/s (7.2 m/s pour 14 nœuds)
- S = Surface projetée du foil en m2,
- ρ = masse volumique de l’eau en kg/m3, soit 1025 kg/m3
- Cz = coefficient de portance (par exemple 0,35)
On constate que deux paramètres sont prépondérants, la vitesse d’évolution du foil dans le fluide (l’eau) car elle s’exprime au carré dans la formule et le Cz (coefficient de portance) qui est relativement instable.
La vitesse d’évolution du foil correspond à la vitesse du bateau.
On perçoit facilement qu’un déplacement lourd, qui ne peut en aucun cas planer, ne pourra pas atteindre une vitesse stabilisée suffisante (elle doit l’être afin de déclencher la phase décollage) qui permettra d’obtenir un « allègement » significatif du bateau. Certes, sur ce type de bateau on peut augmenter l’angle d’incidence afin d’augmenter la portance (force verticale), mais corolairement la trainée s’amplifiera (vecteur dirigé vers l’arrière, donc frein). Le ratio Portance / Trainée est alors trop défavorable.
Le Cz, (Coefficient de Portance), dépend à la fois du profil aérodynamique (généralement des profils NACA), de l’homogénéité du fluide et de l’angle d’incidence, c’est à dire du calage du foil (comme on oriente une voile en la bordant plus ou moins).
L’architecte recherchera le meilleur compromis Portance / Trainée en calant le foil sur le bateau (il fixe l’angle d’incidence). On pourrait imaginer que le calage puisse être réglable comme c’est le cas sur les AC 72, AC45 et sur le MOTH, mais c’est compliqué techniquement (la méthode appliquée sur le MOTH n’est pas transposable). Ensuite le pilotage devrait être asservi, ce qui complexifie encore l’idée. Usuellement le Cz est de 0.30 à 0.35.
| Portance (lift) | ρ | Cz | S m2 | V en Nœuds | V m/s | V2 |
| 78 daN | 1025 | 0.3 | 1.20 | 4 | 2.06 | 4.23 |
| 313 daN | 1025 | 0.3 | 1.20 | 8 | 4.12 | 16.97 |
| 704 daN | 1025 | 0.3 | 1.20 | 12 | 6.18 | 38.19 |
| 957 daN | 1025 | 0.3 | 1.20 | 14 | 7.20 | 51.87 |
| 1411 daN | 1025 | 0.3 | 1.20 | 17 | 8.75 | 76.48 |
Évolution du ratio Déplacement / Longueur
Continuons avec le voilier de 53’ de déplacement 9000 kg et de LFLOT=16 m. Le Ratio Déplacement / Longueur en unités homogènes est égal à DLR (racine cubique du déplacement) / LFLOT, soit :
- En navigation archimédienne : DLR Archimédien = (9000)1/3 / 16 = 1.300
- En prenant en compte un « lift » qui soulage le bateau de 1000 kg et en considérant que LFLOT diminue de 30%, ce ratio devient :
DLF Foiler = (8000)1/3 / (16*0.7) = 1.780
On constate qu’avec l’action du foil le bateau tend de plus en plus vers un déplacement léger, donc potentiellement plus rapide. Pour s’en convaincre imaginons qu’au portant, il soit possible d’alléger le bateau d’une tonne ! Et aussi de diminuer la surface mouillée, etc …

Quel avenir pour les foils sur un monocoque ?
La réponse est compliquée tant elle dépend de paramètres que l’architecture navale ne maitrise pas entièrement. On peut imaginer trois groupes de réponses :
- Les réponses scientifiques qui relèvent du domaine de l’architecture :
- quel type de déplacement pour le monocoque ?
- Quel type de voilier (prototype, racer-cruiser) ?
- Quel type de foil ?
- L’introduction du foil dans les règles de classe :
- autorisée ou refusée (évolution d’un monotype),
- taxation dans le cas de règle de jauge pour la course à handicap, telle l’IRC,
- règles de classe rendant contraignante l’implantation de foils.
- L’implantation dans le bateau :
- le coût du foil et du puits,
- le volume pris dans le bateau,
- le poids,
- les impacts dans les calculs de structures.
Le voilier de régate de demain sera-t-il proche de ce dessin du Cabinet FARR YACHT DESIGN ?

Comment une jauge doit taxer un ou plusieurs foils ?
Toute règle de jauge, possède une philosophie qu’elle applique dans ses orientations et ses choix. Par exemple on peut rappeler les grandes lignes de cette philosophie dans le cas de l’IRC :
- L’IRC n’interdit rien pour peu que le flotteur reste un monocoque et respecte certaines règles de sécurité,
- L’IRC ne pénalise jamais un équipement, comme elle ne tient pas compte de son utilisation aléatoire,
- L’IRC taxe le plus équitablement possible chaque équipement et/ou chaque paramètre qui sont reconnus comme étant des éléments qui favorisent un gain de vitesse. Mais elle peut « favoriser » le développement d’un élément ou d’un équipements comme cela a été le cas avec le spinnaker asymétrique
- Le calcul de chaque taxation ne prend pas en compte la performance de l’équipement et/ou du paramètre au sens du VPP (Velocity Prediction Program). Par exemple l’IRC (comme toutes les jauges) taxe la surface d’une voile, mais en aucun cas ne prend en compte le volume de la voile, le tissu etc.
- L’IRC ne taxe pas l’intelligence des architectes. Libre à eux de dessiner des appendices innovants, des carènes performantes, etc.
- L’IRC ne taxe pas le savoir-faire des skippers.
Ceci dit, deux méthodes sont envisageables pour taxer les foils, et c’est vrai pour tout équipement :
Méthode 1
On recherche un algorithme avec l’espoir qu’il simulera et évaluera le plus justement possible l’apport de performances qu’apportent les foils. Un tel algorithme, obligatoirement compliqué, devra prendre en compte la carène, la voilure, évidemment le ou les foils (dont le profil NACA utilisé) et faire évoluer ces volumes et ces masses dans deux fluides totalement différents (leurs masses volumiques sont respectivement de 1.025 kg/m3 et 1025 kg/m3 soit un ratio de 1000) sans que la position du bateau soit définie parfaitement et constante … Une sorte de VPP-FOILS.
En supposant qu’elle aboutisse, cette méthode permet de concevoir un produit (un foiler par exemple) et d’en connaître les performances afin de proposer ce produit à un éventuel client. Mais cette méthode n’est pas une jauge, elle est simplement un outil d’évaluation.
Pour pouvoir être utilisé comme une Jauge, il faut que le potentiel de vitesse calculé pour chaque bateau en fonction de sa forme, de ses foils, de sa voilure soit converti en un coefficient qui traduira cette prédiction de vitesse. Au final cet outil de simulation scientifique évaluera et notera, le travail de l’architecte, comme le bassin de carène le fait pour une maquette.
Méthode 2
Cette approche est totalement différente. Elle considère que le foil (sa partie active) est l’élément principal du calcul. Elle limite les mesures du foil à son envergure active (Ev) et à la largeur de sa corde (Co). Ensuite elle calcule la surface active (S) du foil (Ev * Co).
Les paramètres généraux du bateau permettent aussi de calculer sa vitesse archimédienne potentielle, mais aussi son aptitude au planning (ratio déplacement/longueur, ratio surface/déplacement, etc). En combinant ces deux entités on peut déterminer une Vitesse potentielle de Planning (Vp). Mais en aucun cas ce n’est pas une analyse « VPP » de la carène.
Je rappelle que deux bateaux peuvent avoir des dimensions et des ratios identiques et avoir des vitesses très différentes, la différence revenant au génie de l’architecte.
A partir des 3 paramètres suivants :
- (S) corrélé par un calcul de l’élancement du foil (Ev² / S). (S) résulte du choix de l’architecte
- (Cz) 0.35 par exemple, la jauge fixe cette valeur de manière pragmatique. elle est évolutive dans le temps
- (Vp), vitesse détude fixée par la jauge d’après les paramètres de base du bateau,
on calcule le potentiel de portance de ce bateau : P = ½ * ρ * Cz * S * Vp2
Ce potentiel de portance représente la valeur théorique de « l’allègement » du bateau à la vitesse d’étude (Vp). Tout ou partie de cette portance peut-être prise en compte dans le calcul de la taxation des foils. A partir de cette évaluation, un coefficient multiplicateur est intégré dans la formule de Jauge.
Avec cette méthode, c’est l’architecte qui est responsable des performances du dessin des foils et de leurs implantations sur le bateau. C’est lui qui connaît exactement le potentiel de vitesse de son projet à toutes les allures. Il utilise à la fois les VPP et les outils de CFD, donc il est à même de dessiner un foil optimum, dont la forme mais surtout le calage (incidence) et le profil (NACA) seront en accord avec le bateau qu’il dessine.
L’architecte a évidement rapidement une idée de la taxation de son foil par la jauge. Enfin presque, car s’il sait que la surface et l’allongement sont pris en compte, il ne connaît pas exactement la vitesse potentielle de planning (Vp) utilisée par la jauge. Toutefois il a une idée de cette vitesse, à partir de ses VPP.
En fait cette méthode de taxation des foils est identique à celles utilisées par les toutes les jauges pour taxer, par exemple, les voiles. On mesure chaque voile, on calcule la surface et on introduit la racine carrée de cette surface en la corrélant par un facteur d’élancement dans la formule de jauge.
A aucun moment une jauge, quelle qu’elle soit, ne prend en compte dans ses calculs les profils de la voile, le ronds de guindant, les angles d’attaque, etc. Même les jauges qui utilisent des VPP prennent le foc comme une forme triangulaire. Aucun artifice (par exemple les rentreurs de pont d’amure de focs) n’est introduit dans le modèle de calcul.
Cette Méthode 2 laisse l’imagination (l’architecte) dessiner les appendices sans autre contrainte que de savoir que seuls la surface et l’allongement seront utilisés pour taxer l’utilisation de foil(s).
Conclusion
L’apparition des foils est intéressante, car elle ouvre la porte de l’innovation dans l’architecture navale et donc la conception des voiliers racer-cruiser.
Rendre les monocoques plus « funs » et plus vivants en utilisant des appendices qui devraient rester abordables financièrement est une évolution de l’histoire des régates qu’il faut saisir.
Quand je vois le travail qui a été réalisé et qui évolue toujours sur les MOTH et d’autres supports, je me dis que beaucoup de choses restent à inventer sur les monocoques lestés.
Est-ce donc irréaliste de penser que les Monocoques lestés puissent rêver de s’extraire quelque peu des flots ?
Jean SANS – 7 juin 2016.

